deep learning
整理一下上课的笔记,不然全都会忘了去
无监督学习
self organizing map 简称SOM算法
大意:给定一个向量$v_{k}$,寻找到距离最近的神经元
找到最接近的神经元
更新$n_{i}$
wikipedia上一张很形象的图片:
蓝色斑点是训练数据的分布,小白色光盘是从该分布中抽取的当前训练数据。首先(左),SOM节点任意地位于数据空间中。选择最接近训练基准的节点(以黄色突出显示)。它被移向训练数据,因为(在较小程度上)是它在网格上的邻居。在多次迭代之后,网格倾向于近似数据分布(右)。

有监督学习
数学知识
特征向量
线性代数中的特征向量:
对于一个给定的方阵A,它的特征向量v经过线性变化之后,得到的新向量仍然与原来的v保持在同一条直线上,但其长度或方向也许会改变,即:
此时$v$就是矩阵$A$的特征向量,$\lambda$就是对应的特征值
进一步:在一定条件下,一个变换可以由其特征值特征向量完全表述,也就是说,所有的特征向量组成了这向量空间的一组基底。
一个特征空间是具有相同特征值的特征向量与一个同维数的零向量的集合,比如$E_{\lambda }=\left \{ u\in V | Au=\lambda u\right \}$即为线性变化$A$中以$\lambda$为特征值的特征空间
抽象概念不容易理解,举几个栗子:
- 恒等变换$I$的特征向量可以看到所有的特征向量都是恒等变换$I$的特征向量,恒等变换的特征空间只有一个就是整个空间
- 类似的,数乘变换$\lambda I$的特征向量也是所有的非零向量,因为按照定义:
感知器
看张图:

数学表述为:$t = f(\sum _{i=1}^{n} w_{i}x_{i} + b) = f(\mathbf{w}^{T} \mathbf{x})$
f函数的表达式:
$\mathbf{x} = \left [ x_{1}\, x_{2} … \, x_{n} \, 1 \right]^{T}$, $\mathbf{w} = \left [ w_{1}\, w_{2} \, …w_{n} \, b \right]^{T}$
如何训练?
我们来看一个训练与运算的demo1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45import numpy as np
def load_data():
'''
加载数据,input_data和labels对应
'''
input_data = [[1, 1], [0, 0], [1, 0], [0, 1]]
labels = [1, 0, 0, 0]
return input_data, labels
def train_pre(input_data, y, iteration, rate):
'''
训练,更新w和b
'''
unit_step = lambda x: 0 if x < 0 else 1
w = np.random.rand(len(input_data[0]))
bias = 0.0
for i in range(iteration):
samples = zip(input_data, y)
for (input_i, label) in samples:
result = input_i * w + bias
result = float(sum(result))
y_pred = float(unit_step(result))
w = w + rate * (label - y_pred) * np.array(input_i)
bias = rate * (label - y_pred)
return w, bias
def predict(input_i, w, b):
'''
预测
'''
unit_step = lambda x: 0 if x < 0 else 1
result = input_i * w + b
result = sum(result)
y_pred = float(unit_step(result))
print(y_pred)
if __name__ == "__main__":
input_data, y = load_data()
w, b = train_pre(input_data, y, 20, 0.01)
predict([1, 1], w, b)
我们很惊讶地发现一个如此简单地模型竟然不可思议地完成了这个任务。
数据更新:
$w(j) := w(j) + \alpha (y-f(x))x(j) (j = 1,…n)$
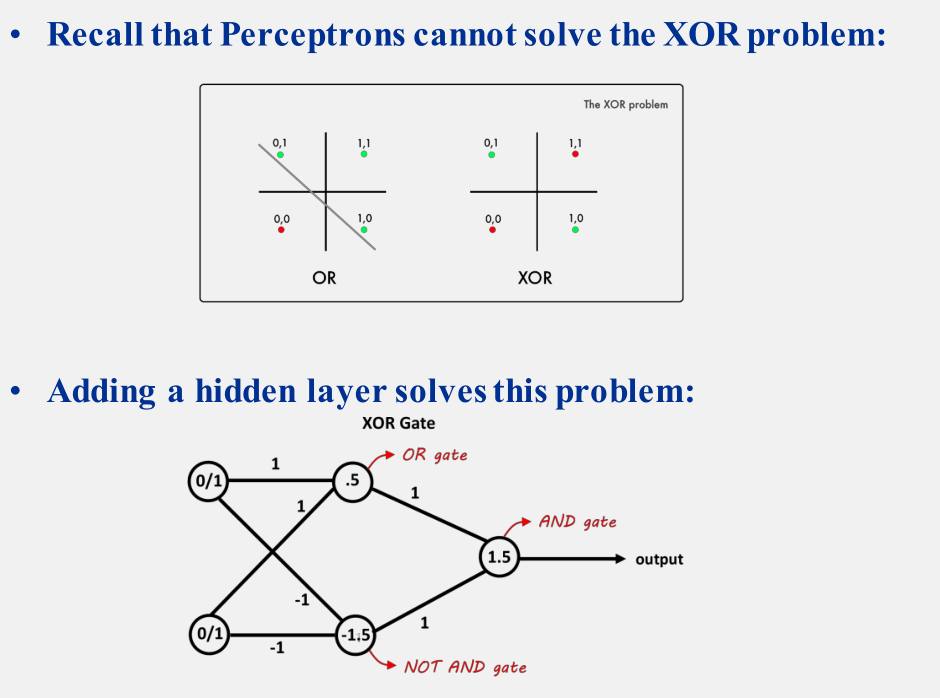
异或问题
当时老师上课时候提到异或问题是不可解的,后来查了一下资料才明白在神经网络发展的早期,异或问题确实是不可解的,不过通过加入隐藏层使得异或问题能够有了新的解法
如下图:
复习的时候才注意到原来老师提到了通过加入隐藏层的方式来解决异或问题